Shady Puzzle Walkthrough

There's a new online game that I first came across while reading MyPaper. You can find the website here.

Be careful because that game is very addictive. Normally when I meet games like this I try to just plunge into it for 3-4 days in a row, playing it for 6 hours a day, before I get sick of it, and then it doesn't bother me again.

When I Google it the autocomplete has "shady puzzle walkthrough" on it, so I suppose some people out there are thinking about how to solve this thing. Well basically if you can't solve the puzzle, you shouldn't be trying to solve it. (Then again, if you have already figured out how to solve the puzzle you shouldn't be trying to solve it either) But I think I should share what I learnt.

In this account, rows will be numbered 1 to 8 from top to bottom. Similarly, column 1 is the leftmost, and column 8 will be the rightmost. I will usually consider 1 column / 1 row at the time. So the 4th square of the column will be the 4th from the top, the 3rd square of the row will be 3rd from the left. etc etc etc.



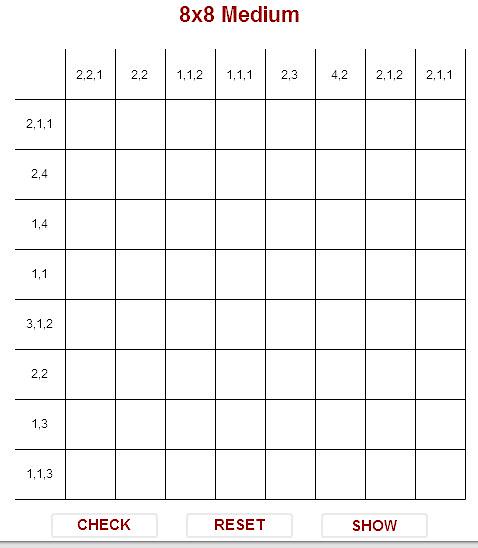
This is the puzzle we'll be solving.

First fill in all those that you can deduce immediately.



Row 5 (3,1,2) is a giveaway.

For row 3 (4,1), the leftmost position of the 1 is starting at square 1. Therefore the leftmost possible position of the 4 is starting at square 3. The rightmost position of the 4 is starting at square 5. In any case, squares 5 and 6 are shaded. So put that in.

Same logic for rows 8 and 2. Same logic for column 1.

Let’s call this the Law of Locus Invariance, ie whether you slide a large block to the left or right, there are always certain squares that are covered by the block. Therefore large blocks are your friend.





The second principle is that if you have filled in a square at the edge, then it is to your advantage. You can deduce the position of the entire block from that square. Look at row 2: the leftmost square has been filled in. Therefore the 2 is all the way to the left. Then fill in the block, and put in 1 blank for good measure. In the same way, you would have done the same for the bottom most squares for columns 6 and 7.

I’ll call this the Law of the edge.




In column 6, you would have deduced the position of the 4 long block. So mark it in. Notice that this means that in row 4 (1,1), there is a square marked in. It’s obvious that the square is a 1 long block. So mark in the blanks. Similarly, in column 5, the block from row 2 to 3 is the “2” of the “2,3”. So mark in the blanks.

This is a different version of the law of the edge. Always mark in the margins of completed blocks with blanks. They will be useful.

Another more subtle application of the law of the margin: look at column 2 (2,2): rows 2 and 5 are marked in. Are they in the same block? No, because none of the blocks are 3 long or more. So they are part of 2 different 2 blocks. Because the bottom most block will never be as low as rows 7 or 8, you can blank those rows out.

Be careful when you are trying to guess which block a filled in square belongs to. Look at row 1 (2,1,1). Square at column 6 is shaded in. Does it belong to the right “1” or the centre “1”? You don’t know. The only thing you know, from counting your squares, is that it doesn’t belong to the “2”. Do not make any hasty conclusions. But you do know that it is part of a 1, so you can blank out the margins.



Fill in column 7 because you know that row 1 is blank.

After this, there’s a lot to be deduced from counting your blocks. Look at row 6. Squares 6 and 7 are blank. There are only 2 blocks in that row, so square 8 is also blank. So your (2,2) fits just nicely into the first 5 squares. Fill that in.

Look at column 1. From block counting, squares 5 and 6 are part of the middle “2”. And therefore square 8 is the “1”.



For column 3, the “2” must be squares 7 and 8. Fill them in, and put in the blanks at the margin. For column 5, you know where your 2 and 3 is, so fill that in. You now have enough information to complete rows 7 and 8. In column 8, you have filled in both the “1”s, so the 2 is in squares 1 to 3. Use the law of invariant locus to fill in square 2.



Finish off row 2 and row 4. Then deduce that for row 3, the “4” is squares 5 to 8. Then finish column 8.



Finish row 1. Then use the law of the edge to finish columns 1 and 2. Then complete column 3. Then we have solved the puzzle by logical deduction alone without any need to do trial and error.

What happens when none of the techniques used (locus invariance, law of edge, block counting) can get you any further? Then you will have to use trial and error. What I do is to select a strategic square to guess. Something, that when filled in or blanked out will lead to a whole chain of deductions. And if I meet with a contradiction, then I know that my initial guess was wrong, I go back to the beginning with the additional info of what that square was. (ie if I guessed the square was black and I’m wrong, I now know that it’s white.)

The other way - and this is often what I do when the board is very sparse (ie very few black squares). I just play around with strips of paper (or drag shaded squares around on MS Excel). I can play columns and rows. ie I drag blocks left and right along the rows, and try to make it such that it agrees with the requirements stated on the columns. Then there's a lot of trial and error involved, but much lesser calculation and logic.